題目在 https://zerojudge.tw/ShowProblem?problemid=f990
思路是先找一個離答案夠近的點, 然後在y=mx+k這條線上去找更佳的解.
我用所有點的重心的X值,來算出線上的Y值, 這(X,Y)就當作夠近的點.
while(j<n){
scanf("%d %d",&xy[j][0], &xy[j][1]);
xall+=xy[j][0];
j++;
}
double x0= float(xall)/n; //所有的點的重心的x
double y0= x0*m+k;第一步的步距delta我訂為5, 下一步位置就是(X+5, m(X+5)+k)), 如果距離的總和變大, 表示走過頭了, 就換個方向, 並減半每步的距離. 這樣來來回回的走,當步距小於0.00001程式結束.
範例的測試可以看出步距delta愈來愈小, 和換方向的過程, x也逐漸逼近0.5
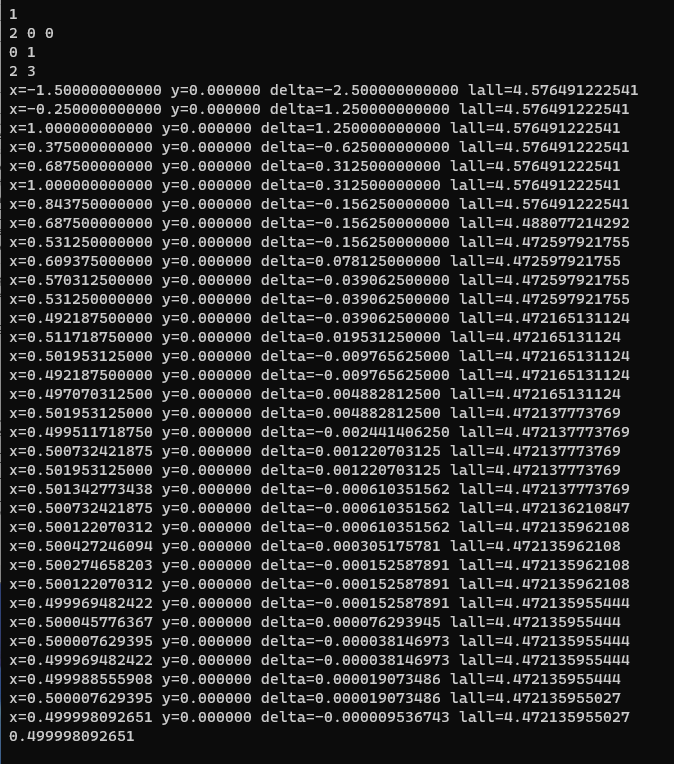
程式如下
#include <stdio.h>
#include <math.h>
#include <cmath>
using namespace std;
int xy[1000000][2];
double getL(double xl, double yl) { return sqrt(xl*xl+yl*yl); }
int main(){
int t, n, m, k;
scanf("%d", &t);
scanf("%d %d %d", &n, &m, &k);
int i=0;
int j;
long long xall;
while (i++<t){
j=0;
xall=0;
while(j<n){
scanf("%d %d",&xy[j][0], &xy[j][1]);
xall+=xy[j][0];
j++;
}
double x0= float(xall)/n;
double y0= x0*m+k;
double delta=5.0; //第一步的步距5
double lall=0; //計算第一次距離和
for(j=0;j<n;j++){
lall+=getL(x0-xy[j][0], y0-xy[j][1]);
}
//開始逼近,當步距小於0.00001程式結束
while(fabs(delta)>0.00001){
double lpall=0;
double xp,yp;
for(j=0;j<n;j++){
xp=x0+delta;
yp=xp*m+k;
lpall+=getL(xp-xy[j][0], yp-xy[j][1]);
}
if(lall < lpall){ //走過頭了, 就換個方向, 並減半每步的距離
delta=-delta/2;
}else{ //沒走過頭, 更新距離和
lall=lpall;
}
x0+=delta;
y0=x0*m+k;
printf("x=%0.12f y=%f delta=%0.12f lall=%0.12f\n",x0,y0,delta,lall);
}
printf("%0.12f\n", x0);
}
}