zerojudge b421. 01077 – The Sky is the Limit 強化

題目在 https://zerojudge.tw/ShowProblem?problemid=b421

這題是在計算天際線的長度. 我看他的AC人數很少,就來試試看, 其中有幾個地方卡了很久. 如果你沒過, 先看看是不是也是這幾個地方. 說不定解決後就成功了.

參數的X,H,B都大於零, 卻不代表山腳的X座標也一定大於0. 如果沒注意到測資#3不會AC.
計算長度或焦點時的變數, 如果你用float, 頂多測資#0,#3 AC. 沒過的答案誤差甚至高達二十幾. 我用double來計算, #1,#2,#4一下就過了. 至於使用long double就沒有必要了.
如果想不通哪裡寫錯, 最好能用電腦畫出來看看,像下面的圖馬上能找到藍色的天際線有沒有算錯. 不然看一堆數字搞得頭昏眼花, 要怎麼除錯?
演算法要夠快, 判斷有沒有交點和計算交點都要快. 我想了兩種算法後, 才找到夠快的算法. #5測資是大魔王, 要計算最久, 不夠快絕對沒辦法AC.

資料結構

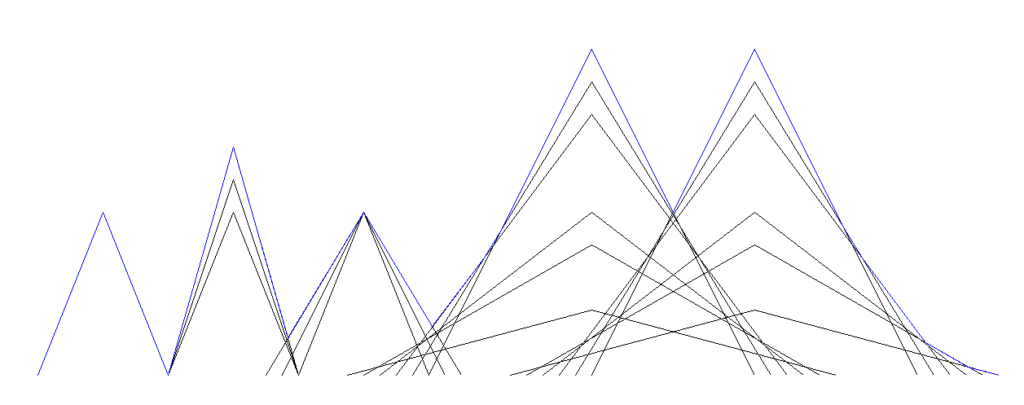
我用NODE來儲存每個需要計算的點. 一座山基本就有三個NODE. 每個NODE有座標X,Y和斜率M. 斜率就是這個NODE座標右邊的那條線的斜率. N1的M就是邊E1的斜率, N2的M就是邊E2的斜率, N3的M就是山底的水平線的斜率0.

class NODE{
	public:
		double X;
		double Y;
		double M;

		void Set(double x,double y,double m){
			X=x;
			Y=y;
			M=m;
		}

		double F(double x){
			return (x-X)*M+Y;
		}

		NODE *getIntersectionNODE(double nx, double nm);
};

class Mountain{
	public:
	  NODE N1,N2,N3;

	  void Set(double x, double h, double b){
		double XL=x-b/2.0;
		double XR=x+b/2.0;
		double M=2*h/b;
		N1.Set(XL,0,M);
		N2.Set(x,h,-M);
		N3.Set(XR,0,0);
	  }
};

C++

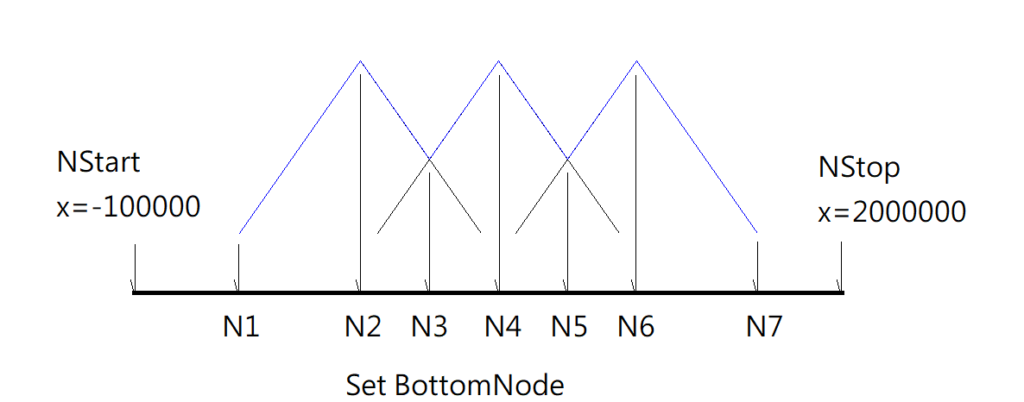
天際線用set來儲存每個NODE指標, 用NODE的X來排序, 因為天際線上的每一NODE剛好會對應在山底的一點. 下圖的案例是三座山的天際線有七個NODE. 演算法就是用三座山的九個NODE算出BOTTOM的七個NODE.

class CompareX{
	public:
		bool operator()(NODE const *a, NODE const *b) const {
			return a->X<b->X;
		}
};

set <NODE *,CompareX> bottom_node;

C++

演算法

每次加入一座山時, 就在這座山的範圍內N1~N3去BOTTOM的set裡找出相關的NODE來計算是否具有交點, 如果有交點就計算出交點, 如果交點上方沒有被遮住(Y座標比較大), 那他就是新的天際線的點, 把他所遮住的舊天際線的點移除, 再把他加入BOTTOM_NODE.

我把每座山分成五個部分N1, E1, N2, E2和N3(見圖二). 每個部分都要判斷有沒有相交, 有就計算交點.

為了避免影響每座山的計算, 新算出來的天際線的NODE都先放在add_record, 要移除的NODE都先放在remove_record, 五個部分都算完後, 再一次全部更新.

加入天際線的NODE有個原則, 因為BOTTOM_NODE裡可能已有相同的X, 所以要先搜尋一下. 如果有的話, Y較高的NODE留下, 如果Y相等, 斜率M較高的NODE留下.

list<NODE*> remove_record;
list<NODE*> add_record;

void AddRecord(NODE *n){
	auto p=bottom_node.find(n);
	if(p != bottom_node.end()){
		if((*p)->Y<n->Y){
			(*p)->Y=n->Y;
			(*p)->M=n->M;
		}else if((*p)->Y==n->Y){
			if((*p)->M<n->M){
				(*p)->M=n->M;
			}
		}
	}else{
		bottom_node.insert(n);
	}
}

void ButtomNodeAddMountain(NODE *N1, NODE *N2, NODE *N3){
		remove_record.clear();
		add_record.clear();

		AtNode(N1);
		AtEdge(N1, N2, N1->X);
		AtNode(N2);
		AtEdge(N2, N3, N3->X);
		AtNode(N3);

		for(auto p:remove_record){
			bottom_node.erase(p);
		}
		for(auto p:add_record){
			AddRecord(p);
		}
	}

C++

每個部位怎麼知道有沒有交點呢? 就是比較天際線的每個NODE的Y值和五個部位的Y值. 下圖四中, 新山在N1的Y值本來比天際線小, 在N2的Y卻變成比較大了. 那這個N2和前一個N1之間就存在一個交點. 同理, Y值由大變小也是存在交點.

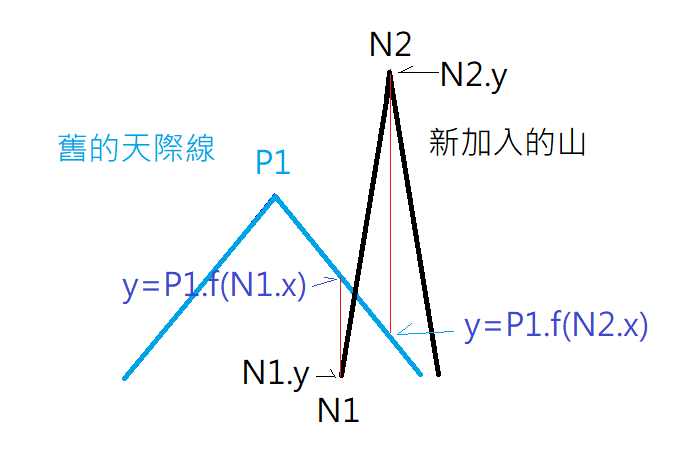
怎麼計算交點座標呢? 為了算的快,我利用山的N1或N3的Y座標為0來加快計算.

假設P1座標(X,Y),斜率M. N1座標(nx,0)斜率nm, 可求得交點座標(x,y), 公式如下:

x= (nx*nm-X*M+Y)/(nm-M)
y= (X-nx)*nm;

這公式也可以計算N2和N3之間的交點.但是N2的Y不為0, 所以用N3的X和N2的M來算,答案是一樣的.

斜率相同的情況,不是共線就是無交點, 所以傳回NULL.

NM是NodeManager, 主要用來管理NODE的記憶體,因為交點的NODE的記憶體是new出來的, 所以要在程式後面釋放掉. 細節就省略了.


NODE* NODE::getIntersectionNODE(double nx, double nm){
	if(M==nm)
		return NULL;

	double large = (M>nm? M:nm);
	if(Y==0 && M==0){
		return NM.Add(nx,0,large);
	}
	double x= (nx*nm-X*M+Y)/(nm-M);
	double y= (x-nx)*nm;
	return NM.Add(x,y,large);
}

C++

最後來到五個部分(N1,E1,N2,E2,N3)的比較, 其中N1,N2,N3這三個NODE的寫法都一樣, 就是找有沒有比他高的Y, 沒有的話就加入BOTTOM_NODE;

void AtNode(NODE *N){

	auto p = bottom_node.upper_bound(N);
	p--;

	double y=(*p)->F(N->X);
	if(y<=N->Y){
		add_record.push_back(NM.Add(N->X,N->Y,N->M));
	}
}

C++

其它兩個E1和E2寫法也一樣, 但是E1是N1的Y為0, E2卻是N2的Y為零, 所以Y為0時的X值就用參數Xb傳給它.

void AtEdge(NODE *N1, NODE *N2, double Xb){

	auto start = bottom_node.upper_bound(N1);
	start--;

	int Sign;
	double y=(*start)->F(N1->X);
	if(y>N1->Y)
		Sign=-1;
	else if(y<N1->Y)
		Sign=1;
	else
		Sign=0;

	auto stop = bottom_node.upper_bound(N2);

	while(start!=stop){
		auto p = start;

		p++;
		double N1y2=N1->F((*p)->X);
		if(N1y2>(*p)->Y){
			if((*p)->X>=N1->X && (*p)->X<N2->X){
				remove_record.push_back(*p);
			}
			if(Sign!=1){
				Sign=1;
				p = start;
				NODE *n=(*p)->getIntersectionNODE(Xb,N1->M);
				if(n && N1->X<=n->X && n->X<N2->X && (*p)->X<=n->X){
					add_record.push_back(n);
					}
				}
		}else if(N1y2<(*p)->Y){
			if(Sign!=-1){
				Sign=-1;
				p = start;
				NODE *n=(*p)->getIntersectionNODE(Xb,N1->M);
				if(n && N1->X<=n->X && n->X<N2->X && (*p)->X<=n->X){
					add_record.push_back(n);
					}
				}
		}else{  //N1y2==(*p)->Y
			if((*p)->X<N2->X){
				add_record.push_back(NM.Add((*p)->X,(*p)->Y,N1->M));
			}
		}
		start++;
	}

}

C++

這樣程式就完成了, 這簡化版目前似乎夠快了,只花0.2S. 如果N1,N2,N3和E1,E2都分開處理可以更快.

只需要99ms. 但是有點複雜,就不寫在這了.

以下是完整程式碼.

#include <iostream>
#include <list>
#include <set>
#include <math.h>
using namespace std;


class NODE{
	public:
		double X;
		double Y;
		double M;

		NODE(){
			X=0;
			Y=0;
			M=0;
		}

		void Set(double x,double y,double m){
			X=x;
			Y=y;
			M=m;
		}

		void Clear(){
			X=0;
			Y=0;
			M=0;
		}

		double F(double x){
	        return (x-X)*M+Y;
		}

		NODE *getIntersectionNODE(double nx, double nm);
};

class NodeManager {
	private:
		list <NODE *> L;
	public:

		NODE *Add(double x, double y, double m){
			NODE *N=new NODE();
			N->Set(x,y,m);
			L.push_back(N);
			return N;
		}

		void Clear(){
			for (NODE *p : L) {
				delete p;
			}
			L.clear();
		}

		~NodeManager(){
			Clear();
		}
};

NodeManager NM;

NODE* NODE::getIntersectionNODE(double nx, double nm){
	if(M==nm)
		return NULL;

	double large = (M>nm? M:nm);
	if(Y==0 && M==0){
		return NM.Add(nx,0,large);
	}
	double x= (nx*nm-X*M+Y)/(nm-M);
	double y= (x-nx)*nm;
	return NM.Add(x,y,large);
}

class CompareX{
	public:
		bool operator()(NODE const *a, NODE const *b) const {
			return a->X<b->X;
		}
};

set <NODE *,CompareX> bottom_node;

class Mountain{
	public:
	  NODE N1,N2,N3;

	  void Set(double x, double h, double b){
		double XL=x-b/2.0;
		double XR=x+b/2.0;
		double M=2*h/b;
		N1.Set(XL,0,M);
		N2.Set(x,h,-M);
		N3.Set(XR,0,0);
	  }
};

void AddRecord(NODE *n){
	auto p=bottom_node.find(n);
	if(p != bottom_node.end()){
		if((*p)->Y<n->Y){
			(*p)->Y=n->Y;
			(*p)->M=n->M;
		}else if((*p)->Y==n->Y){
			if((*p)->M<n->M){
				(*p)->M=n->M;
			}
		}
	}else{
		bottom_node.insert(n);
    }

}

list<NODE*> remove_record;
list<NODE*> add_record;

void AtNode(NODE *N){

	auto p = bottom_node.upper_bound(N);
	p--;

	double y=(*p)->F(N->X);
	if(y<=N->Y){
		add_record.push_back(NM.Add(N->X,N->Y,N->M));
	}
}


void AtEdge(NODE *N1, NODE *N2, double Xb){

	auto start = bottom_node.upper_bound(N1);
	start--;

	int Sign;
	double y=(*start)->F(N1->X);
	if(y>N1->Y)
		Sign=-1;
	else if(y<N1->Y)
		Sign=1;
	else
		Sign=0;

	auto stop = bottom_node.upper_bound(N2);

	while(start!=stop){
		auto p = start;

		p++;
		double N1y2=N1->F((*p)->X);
		if(N1y2>(*p)->Y){
			if((*p)->X>=N1->X && (*p)->X<N2->X){
				remove_record.push_back(*p);
			}
			if(Sign!=1){
				Sign=1;
				p = start;
				NODE *n=(*p)->getIntersectionNODE(Xb,N1->M);
				if(n && N1->X<=n->X && n->X<N2->X && (*p)->X<=n->X){
					add_record.push_back(n);
					}
				}
		}else if(N1y2<(*p)->Y){
			if(Sign!=-1){
				Sign=-1;
				p = start;
				NODE *n=(*p)->getIntersectionNODE(Xb,N1->M);
				if(n && N1->X<=n->X && n->X<N2->X && (*p)->X<=n->X){
					add_record.push_back(n);
					}
				}
		}else{  //N1y2==(*p)->Y
			if((*p)->X<N2->X){
				add_record.push_back(NM.Add((*p)->X,(*p)->Y,N1->M));
			}
		}
		start++;
	}

}

void ButtomNodeAddMountain(NODE *N1, NODE *N2, NODE *N3){
		remove_record.clear();
		add_record.clear();

		AtNode(N1);
		AtEdge(N1, N2, N1->X);
		AtNode(N2);
		AtEdge(N2, N3, N3->X);
		AtNode(N3);

		for(auto p:remove_record){
			bottom_node.erase(p);
		}
		for(auto p:add_record){
			AddRecord(p);
		}
	}

Mountain M[10000];

int main() {

	double N, X, H, B;

	int CaseNo=1;


	while(1){
		cin >> N;
		if(N==0)
			break;

		bottom_node.clear();
              bottom_node.insert(NM.Add(-100000,0, 0));
		bottom_node.insert(NM.Add(2000000, 0, 0));
		bottom_node.insert(NM.Add(2000001, 0, 0));

		for(int i=0;i<N;i++){

			cin >> X >> H >> B;

			M[i].Set(X,H,B); //#3pass
			ButtomNodeAddMountain(&M[i].N1,&M[i].N2,&M[i].N3);
		}

		double x1=0,y1=0, L=0;
		for(auto p = bottom_node.begin();p!=bottom_node.end();p++){
			if((*p)->M!=0){
				auto p2=p;
				p2++;
				double XL=(*p2)->X-(*p)->X;
				double YL=(*p2)->Y-(*p)->Y;
				L+=sqrt(XL*XL+YL*YL);
			}
		}

		int R=round(L);
		cout << "Case "<< CaseNo++ <<": "<< R << endl << endl;

		NM.Clear();
		}


	return 0;
}

C++

zerojudge b421. 01077 – The Sky is the Limit 強化

Archives

Categories